CLES

An instrument for monitoring the development

of constructivist learning environments

Peter C Taylor, Barry J Fraser & Loren R White

National Key Centre for School Science and Mathematics

Curtin University, Australia

Paper presented at the annual meeting of the American Educational Research Association, New Orleans, April 1994

abstract

A revised version of the Constructivist Learning Environment Survey (CLES) has been developed for researchers who are interested in the constructivist reform of high school science and mathematics. Constructivist theory and critical theory have been combined to create a powerful interpretive framework for examining science and mathematics teaching. The cognitive focus of the earlier instrument has been broadened by including a concern for the socio-cultural forces that shape the rationality of traditional science and mathematics classrooms. The revised CLES is concerned with the extent of emphasis within a classroom environment on: (a) making science and mathematics seem relevant to the world outside of school; (b) engaging students in reflective negotiations with each other; (c) teachers inviting students to share control of the design, management, and evaluation of their learning; (d) students being empowered to express concern about the quality of teaching and learning activities; and (e) students experiencing the uncertain nature of scientific and mathematical knowledge. The revised CLES was trialled in an innovative empirically-oriented mathematics classroom. The results of the study, which combined statistical analyses and interpretive inquiry, confirmed the practical viability of the CLES and generated important insights into use of learning environment questionnaires in classrooms undergoing constructivist transformation.

Introduction

At AERA in 1991, we presented a new learning environment instrument — the Constructivist Learning Environment Survey (CLES) — that we had designed to enable teacher-researchers to monitor their development of constructivist approaches to teaching (Taylor & Fraser, 1991). Our goal in designing the original CLES was to provide teachers with an efficient means of learning more about their students' perceptions of the extent to which the classroom learning environment enabled them to reflect on their prior knowledge, develop as autonomous learners, and negotiate their understandings with other students.

Although the original CLES was found to be psychometrically sound with a sample of over 500 high school students in science and mathematics classes, and was found to be very useful in a number of studies (Roth & Bowen, in press; Roth & Roychoudury, 1993, 1994; Watters & Ginns, 1994), we felt that its theoretical framework supported only a weak program of constructivist reform. Our ongoing research program had revealed major socio-cultural constraints to the development of constructivist teaching approaches (Taylor, 1992, 1993, 1994; Taylor & Williams, 1993). We felt that a revised CLES should empower teachers to address these restraints. Subsequently, in the revised CLES we incorporated a critical theory perspective on the socio-cultural framework of the classroom learning environment (Grundy, 1987; Habermas, 1972, 1984), and developed a critical constructivist theoretical framework.

The purpose of this paper is to present the rationale of the revised CLES, especially its critical constructivist theoretical framework, and to discuss what we learned as a result of our attempts to determine the practical viability of the questionnaire. The redesign of the CLES involves the trialling of the questionnaire in high school science and mathematics classrooms. This paper focuses on the results of a collaborative research study (Kyle & McCutcheon, 1984; Watt & Watt, 1982) that involved one of the authors (Loren White) adopting the role of teacher-researcher and introducing an innovatory empirically-oriented mathematics project (The Egg Project) into his Grade 8 mathematics classroom.

Following a brief overview of the field of classroom learning environment, the second section of the paper presents the theoretical framework of critical constructivism that underpins the scales of the revised CLES. The third section discusses the research design of the study which combines quantitative and qualitative approaches to data generation and analysis. The fourth section presents the results of the study which are organised as three interpretive research assertions and evidence that warrants them. In the concluding section, we reflect on the main results and consider their implications for future research involving the use of the revised CLES for monitoring classroom learning environments under transformation.

BACKGROUND: FIELD OF CLASSROOM ENVIRONMENT

Over the previous two decades or so, considerable interest has been shown internationally in the conceptualisation, assessment, and investigation of perceptions of psychosocial characteristics of the learning environment of classrooms at the elementary, secondary, and higher education levels (Chavez, 1984; Fraser, 1986, 1989, 1994; Fraser & Walberg, 1991; MacAuley, 1990). Classroom environment instruments have been used as sources of both predictor and criterion variables in a variety of research studies.

Use of student perceptions of classroom environment as predictor variables in several different countries has established consistent relationships between the nature of the classroom environment and various student cognitive and affective outcomes (Fraser, 1986; Haertel, Walberg & Haertel, 1981; McRobbie and Fraser, 1993). For example, Fraser and Fisher's (1982) study involving 116 Australian science classes established sizeable associations between several inquiry skills and science-related attitudes and classroom environment dimensions measured by the Classroom Environment Scale and the Individualized Classroom Environment Questionnaire. Furthermore, research involving a person-environment fit perspective has shown that students achieve better where there is greater congruence between the actual classroom environment and that preferred by students (Fraser & Fisher, 1983).

Studies involving the use of classroom environment scales as criterion variables have revealed that classroom psychosocial climate varies between Catholic and government schools (Dorman, Fraser and McRobbie, 1994) and between coeducational and single-sex schools (Trickett, Trickett, Castro & Schaffner, 1982). Both researchers and teachers have found it useful to employ classroom climate dimensions as process criteria of effectiveness in curriculum evaluation because they have differentiated revealingly between alternative curricula when student outcome measures have shown little sensitivity (Fraser, 1981; Fraser, Williamson & Tobin, 1987). Research in the USA (Moos, 1979), Australia (Fraser, 1982), The Netherlands (Wubbels, Brekelmans & Hooymayers, 1991), and Israel (Raviv, Raviv & Reisel, 1990) compared students' and teachers' perceptions and found that, first, both students and teachers preferred a more positive classroom environment than they perceived as being actually present and, second, teachers tended to perceive the classroom environment more positively than did their students in the same classrooms. In promising small-scale practical applications, teachers have used assessments of their students' perceptions of their actual and preferred classroom environment as a basis for identification and discussion of actual-preferred discrepancies, followed by a systematic attempt to improve classrooms (Fraser & Fisher, 1986).

Some of the exciting recent lines of classroom environment research which are still in progress involve: investigating the links between and the joint influence of classroom, school, family, and other environments on students' outcomes (Moos, 1991); incorporating classroom environment as one factor in a multi-factor model of educational productivity (Fraser, Walberg, Welch & Hattie, 1987); evaluating and investigating teacher-student interpersonal relationships in the classroom (Wubbels and Levy, 1993); exploring ways in which classroom environment instruments can be used to advantage by school psychologists (Burden & Fraser, in press); incorporating learning environment ideas into teacher education (Fraser, 1993); investigating changes in classroom environment during the transition from elementary to high school (Midgley, Eccles & Feldlaufer, 1991); and incorporating the evaluation of classroom environment in teacher assessment schemes (Heroman, Loup, Chauvin & Evans, 1991).

Critical Constructivist Framework

The original version of the CLES was based on a theory of constructivism that underpins recent research in science and mathematics education that is concerned with developing teaching approaches that facilitate students' conceptual development (Driver, 1988, 1990; Treagust, Duit, & Fraser, in press). This conceptual change research highlights: (1) the key role of students' prior knowledge in their development of new conceptual understandings, especially the problematic role of students' alternative conceptions; and (2) the reflective process of interpersonal negotiation of meaning within the consensual domain of the classroom community.

However, our research on teachers' development of constructivist pedagogies has shown how readily traditional teacher-centred classroom environments can assimilate conceptual change perspectives and remain largely unchanged (Taylor, 1992, 1993, 1994). We have found that the rationality of traditional teacher-centred classrooms is dominated by two cultural myths: (1) an objectivist view of the nature of scientific and mathematical knowledge; and (2) a complementary technical controlling interest that views the curriculum as a product to be delivered. If classroom learning environments are to feature negotiation and meaning-making, then teachers need to be empowered to deconstruct these repressive myths.

Deconstructing Cultural Myths

From an objectivist (or Platonic) perspective, scientific (or mathematical) knowledge seems to exist independently of our minds, to be static and unchanging over time, and to be the embodiment of universal Truths. If this foundationalist perspective represents a true account of scientific and mathematical knowledge, then teachers are entitled to adopt the role of experts whose task is to transmit to their students accurate versions of the universal body of Truths. However, during the second half of this century, the foundational view of knowledge has been challenged and largely discredited by philosophers of science (Feyerabend, 1962; Kuhn, 1962; Polanyi, 1959; Toulmin, 1953) and philosophers of mathematics (Davies & Hersch, 1981; Hersch, 1986; Kitcher, 1984; Kline, 1953, 1980).

In the field of science education, Solomon (1987, 1991) and Tobin (1990, 1993) have made accessible to science educators an alternative view of the nature of scientific knowledge — social constructivism. Likewise, in mathematics education, researchers such as Bauersfeld (1989, 1992) and Ernest (1991, 1992) have developed social constructivist philosophies. The interlinking of science and mathematics education by means of a constructivist philosophy is evident in the work of Bauersfeld, Ernest and Tobin, all of whom have built their theories by adapting von Glasersfeld's (1990, 1993) radical constructivism.

Of course, our scientific and mathematical knowledge must be validated against community norms and, for Solomon (1987), who builds on the sociology of knowledge of Berger and Luckman (1966), this intersubjectivity is achieved by means of negotiating and consensus building, which are activities that are shaped by the social and cultural frameworks within which they occur. For Solomon and Cobb (1989), these activities are undertaken by both professional scientists/mathematicians and students of science/mathematics, within their respective communities.

From a social constructivist perspective, the roles of teachers and students are dramatically transformed. Teachers become mediators of students' encounters with their social and physical worlds and facilitators of students' interpretations and reconceptualisations. A key role is to assist students to problematise and reconstruct their existing conceptions and to determine the viability of their new ideas in the social forums of the classroom and the broader community (e.g., parents). However, the possibility of teachers shaping classroom learning environments in accordance with a social constructivist perspective is dependent on the prevailing curriculum and assessment structure.

The Technical Interest

The philosopher, Jurgen Habermas (1972, 1984), presents three fundamental human interests - technical, practical, emancipatory - that govern our ways of knowing and acting towards one another. He argues that the technical interest, which underpins positivist views of the nature of science, is associated with self-interest, and the control and exploitation of nature. Curriculum theorists who have adopted Habermas's epistemology argue that a technical interest has prevailed as the dominant mythology of the West's education professions for most of this century (Apple, 1979; Giroux, 1983; Grundy, 1987; Schon, 1983). As a result, a professional culture has developed that renders the concept of curriculum in terms of the objectivist metaphor of a container of immutable knowledge — curriculum as product — which the teacher is obligated to deliver. Coupled with the traditional summative assessment policy, a powerful cultural mythology has developed that holds the teacher accountable for the delivery of knowledge to students. It is not surprising, therefore, that in traditional science classrooms the locus of control of learning activities is believed to lie with the teacher (who, in most State-controlled curricula, serves as an agent for an external authority). In these classroom environments, students are required to comply unquestioningly with the teacher's instructional prescriptions and with the prescribed social norms of the classroom environment. At first glance, this curriculum straightjacket seems to offer little prospect for social constructivist teaching approaches to flourish.

The Practical Interest

However, recent developments in curriculum theory are highly compatible with a social constructivist reform agenda in the science classroom. The critical theory of the Habermas (1972, 1984) provides a powerful conceptual framework for understanding the rationality of social institutions, such as schools, and the political interests that are served by traditional notions of curriculum. In essence, Habermas argues that in order for a society to flourish the traditional and predominant technical self-interest in control, prediction and manipulation (often associated with economically-driven exploitative practices) must be counterbalanced by a practical interest in the moral welfare of others and an emancipatory interest in becoming critically aware of cultural myths that distort our understandings of self and others.

In the context of education, a practical interest is associated with understanding and respecting the meaning-perspectives of others, and gives rise to opportunities for students to: (a) negotiate with the teacher about the nature of their learning activities; (b) participate in the determination of assessment criteria and undertake self-assessment and peer-assessment; (c) engage in collaborative and open-ended inquiry with fellow students; and (d) participate in reconstructing the social norms of the classroom. Many of these ideas have been embraced by constructivist mathematics educators (Cobb, 1989). The practical interest might also be expressed in classrooms by means of establishing an open discourse, that is, communication that promotes respect for participants, aims at understanding others' understandings, and legitimates non-coercive actions and self-disclosure of goals, values, frustrations and beliefs (Taylor & Williams, 1993).

The Emancipatory Interest

However, we believe that the activation of a practical interest constitutes only a part of the necessary reform agenda for traditional science and mathematics classrooms. There is a need for an emancipatory interest that gives rise to opportunities for teachers and students to become critically aware of the influence of the repressive myths of objectivism and control that govern the social reality of institutions and classrooms and that constrain the development of open discourses.

We do not believe that it is desirable to try to eliminate the technical interest. It constitutes one of the fundamental ways of knowing and acting that underpin our society. Rather, we advocate the achievement of a more harmonious rationality that is based on a balance between the technical, practical and emancipatory interests. Therefore, in addition to an open discourse, we need to establish a critical discourse that serves to reveal and subject to critical scrutiny the prevailing (invisible) myths that disempower teachers and students from developing more harmonious classroom learning environments.

It was with these goals in mind that we redeveloped the scales of the CLES and trialled it in a high school mathematics classroom.

SCALES OF THE CLES

The revised version of the CLES comprised five scales each of which was designed to obtain measures of students' perceptions of key aspects of their mathematics classroom learning environment. The CLES comprised 40 items arranged in traditional cyclic order.

Personal Relevance Scale

In revising the CLES, we were mindful of the need to assist teachers who are interested in taking their first steps towards developing constructivist pedagogies to develop teaching strategies that aim to account for students' preconceptions. However, we wanted teachers to broaden their pedagogical focus beyond students' abilities to recall accurately previously learned formulae, rules, and laws, and take account of the rich tapestry of experiences that students bring with them from their out-of-school worlds. Consequently, we developed the Personal Relevance scale that is concerned with the perceived relevance of school mathematics to students' out-of-school experiences. We are interested in teachers making use of students' everyday experiences as a meaningful context for the development of students' mathematical knowledge.

Shared Control Scale

From a critical constructivist perspective, we are concerned that students have opportunities to develop as autonomous learners. We believe that this can be achieved partly by providing opportunities for students to exercise a degree of control over their learning that extends beyond the traditional practice of working 'independently' in class on sets of prescribed problems. The Shared Control scale is concerned with students being invited to share control with the teacher of the total learning environment, including the design and management of learning activities, determining and applying assessment criteria, and participating in the negotiation of the social norms of the classroom. It seems to us that the rationale for this scale fits well with the notion of a portfolio culture (Duschl & Gitomar, 1991) that places a major emphasis on students monitoring their own conceptual development.

Critical Voice Scale

Of course, we realise that many teachers will feel constrained, at least in the short-term, by their externally-mandated interest in delivering the curriculum and covering curriculum content. This technical curriculum interest directs teachers' sense of accountability for curriculum implementation away from the classroom and towards external curriculum and assessment authorities. However, we believe that teachers also should be accountable to their students for their pedagogical actions. From a critical theory perspective, which promotes an interest in student empowerment, we would like teachers to demonstrate willingly to the class their pedagogical accountability by fostering students' critical attitudes towards the teaching and learning activities. The Critical Voice scale assesses the extent to which a social climate has been established in which students feel that it is legitimate and beneficial to question the teacher's pedagogical plans and methods, and to express concerns about any impediments to their learning.

Student Negotiation Scale

Although we recognise the importance of the teacher-student negotiations set out in the first three scales, we wish to emphasise in the CLES the importance of developing instructional strategies that promote student-student negotiations as a central classroom activity. The Student Negotiation scale focuses on whether teachers' pedagogical attention extends beyond the traditional social activity of students helping each other to work out the correct answer to a problem. The scale assesses the extent to which opportunities exist for students to explain and justify to other students their newly developing ideas, to understand other students' ideas and reflect on their viability and, subsequently, to reflect on the viability of their own ideas.

Uncertainty Scale

One of the major constraints to constructivist pedagogical reform is the popular myth that Western science and mathematics are universal, mono-cultural (or accultural) endeavours that provide accurate and certain knowledge of objective reality. The myth of certainty implies that mathematical and scientific knowledge exists independently of collective human experience. By contrast, we want teachers to provide opportunities for students to experience the inherent uncertainty and limitations of scientific and mathematical knowledge. The Uncertainty Scale has been designed to assess the extent to which opportunities are provided for students to experience scientific and mathematical knowledge as arising from human experience and values, as evolving and insecure, and as culturally and socially determined.

Items in Revised CLES Scales

As a result of this study, the five scales of the revised CLES were refined and reduced to seven items each. The final version of the revised CLES for use in mathematics classes is provided in the Appendix. The allocation of the 35 items to the 5 scales is shown in Table 1.

Table 1

Allocation of Items to CLES Scales

Scale Item Numbers

Personal Relevance 1 7 13 19 25 30 37

Mathematical Uncertainty 2 8 14 20 26 31 38

Critical Voice 3 9 15 21 27 32 39

Shared Control 4 10 16 22 28 33 40

Student Negotiation 5 11 17 23 29 34 41

Items without their item numbers underlined are scored 5, 4, 3, 2 and 1, respectively, for the responses Almost Always, Often, Sometimes, Seldom and Almost Never. Items with their item numbers underlined are scores in the reverse manner. Omitted or invalid responses are scored 3.

Attitude scale comprising Items 6, 12, 18, 24, 29, 35 and 42. These attitude items are scored in the same way as the CLES items.

The final version of the revised CLES for use in science classrooms has identical scales except that a Scientific Uncertainty scale replaces the Mathematical Uncertainty scale

practical viability of the cles

After redeveloping the five scales of the CLES, we wanted to determine their practical viability. That is, we were interested in finding an answer to the question about whether they could be used to generate meaningful data about students' perceptions. In order to assess the meaningfulness of the CLES data, we needed to generate data from other sources and determine the extent to which the CLES data could be combined with other data to generate a plausible account within a particular context. This need gave rise to the following research question.

Research Question

The main research question of the study was whether the CLES could be used to generate a plausible account of students' perceptions in a constructivist-oriented classroom? An interpretivist warrant for judging the efficacy of the CLES was appropriate because our goal is to provide a means of enabling teachers to understand better the perspectives of their students. The warrant of plausibility recognises that the inquirer's perspective is context-dependent and allows for multiple interpretations to be made. In other words, by using this warrant, we are claiming that multiple learning environments exist in the same physical space.

We were mindful, therefore, of the need to avoid allowing only the traditional warrants of the psychometric paradigm to prevail. We did not wish to fall victim to statistical determinism when evaluating the efficacy of individual items. However, we also were mindful of the need for an inclusive warrant that would enable us to combine qualitative and quantitative data analyses. So, how did we define plausibility? We decided that the warrant of plausibility would comprise the following criteria which allowed us to make judgements about the educational significance of the results of the trial.

• The extent to which the CLES generated intelligible and dependable responses from students.

• The extent to which student responses to groups of items (identified as scales) aggregated in a coherent and meaningful way.

• The extent to which the CLES data were consistent with data from other sources.

Research Methodology

We adopted an interpretive research approach (Erickson, 1986) that enabled us to conduct an in-depth investigation of a single high school mathematics classroom. The revised version of the CLES was trialled in a Grade 8 mathematics class in a government high school in the Perth metropolitan area. The purposes of the trial were to determine the practical viability of the five scales and to reduce the 40-item CLES to a more economical 35 items (i.e., 7 items/scale). An interpretive research approach framed the study and was used to investigate the implications of statistical analyses. For each scale, we calculated: (1) whole-class and small-group mean scores and standard deviations; (2) a Cronbach alpha reliability coefficient; and (3) item-scale correlation coefficients. For the five scales, we calculated a scale intercorrelation matrix.

Major methodological strategies that we attempted to employ for the purpose of safeguarding our warrant of plausibility were drawn from the field of interpretive research (Denzin, 1988; Eisenhart, 1988; Erickson, 1986; Mathison, 1988), and included:

(1) minimising underdetermination of our theorising by employing triangulation in the form of multiple data sources, multiple methods of generating data, and multiple investigators;

(2) avoiding the predominance of our preconceptions by generating emergent research questions and assertions (i.e., grounded theory) and searching for disconfirming evidence;

(3) understanding the context of participants' actions by immersing ourselves in the field;

(4) establishing a rapport with students so that interviews would be informal good conversations; and

(5) avoiding unethical actions by maintaining our concern for safeguarding students' learning opportunities and our guarantees of confidentiality and anonymity.

Nevertheless, we experienced several problems in safeguarding our warrant. Given the time constraints, it was not possible for the participant-researcher to attend all lessons during the 10-week project or to interview students on more than one occasion.

The Teacher-Researcher

We designed a collaborative research study (Kyle & McCutcheon, 1984; Watt & Watt, 1982) in which one of us (Loren White) adopted the role of teacher-researcher in his own classroom. In this role, Loren was a member of the research team and participated in both the ongoing generation and analysis of quantitative and qualitative data. As a teacher, Loren was well-suited to the study. One of his first tasks was to appraise the appropriateness for high school students of the language and content of a draft of the revised CLES. Loren tested the items for sense and clarity with high school students in Grades 8-11 during private study sessions. Discussions with students resulted in several revisions and a modified form of the 40-item CLES (i.e., 5 scales each of 8 items) which was ready for in-depth evaluation with a mathematics class.

We were keen to focus on a class where the teacher was involved in student-centred practices instead of mostly 'stand and deliver' practices. Loren believed that his Grade 8 mathematics classroom might have some of the characteristics of the learning environment assessed by the scales of the CLES. He proposed that a special five-week mathematics activity that he had been planning (that we came to call the 'Egg Project') would be an appropriate context for our study.

The Egg Project asked students to find a simple way to estimate the surface area of an egg. From Loren's perspective, the pedagogy of this project was based on giving students experience with open-ended problem solving and investigation. The students were expected to make choices about processes including the mathematics. As there were no known simple formulations to be 'found' easily in books or to appear miraculously from somewhere, the challenge to students was to be creative, and then validate their methods and results. Loren considered that the project provided opportunities for students to engage in group work, oral and written reports, and evaluation of peers. The project also was an opportunity to give students experience with mathematical modelling, empirical processes, multiple open-ended solutions to problems, and the uncertainty of mathematics.

Framing the Egg Project was Loren's pedagogical intention to integrate his students' experiences in mathematics and science. Throughout the year, he had been collaborating with the Grade 8 science teacher to emphasise the interdependence of the two disciplines. Loren expected the students to use their science experiences to observe, measure, collect and organise data, hypothesise, test, evaluate and theorise. The five-week Egg Project provided his Grade 8 students with the first extended opportunity to engage in these empirical activities in the mathematics classroom.

Currently, Loren is a PhD candidate at Curtin University. At the time of this study, he was teaching part-time at the school in this study. He is an experienced teacher of 13 years, and has 10 years working experience in non-educational environments prior to entering the teaching profession. Loren is aware of many forms of constructivist theories and the associated pedagogical principles put forward by constructivist educational theorists. He accepts the view that the Egg Project meets much of the ideal discursive practices considered necessary by constructivists to enhance learning in a classroom. However, he did not consciously have particular key principles of constructivist theory in mind when developing this project.

The Egg Project evolved from a need to give the students, at this stage in their program of study, an opportunity to synthesise many of their understandings of mathematics and science. This was at the middle of the third term of a four-term school year. Loren's pedagogy comprises a constantly evolving set of ideals arising from his life experiences. Foremost is his desire to consider students as people first and teaching as a collaborative practice with students to help them meet their expectations of school as tempered by the expectations of others, such as parents and community. Constructivism, like many other isms is a useful framework for Loren for rationalising many of his pedagogical principles and for reflecting on classroom practices.

Key components of the Egg Project were its empirical basis for justification, the ongoing discourses between students and with the teacher, and redeemable assessment. The last of these is a process of assessment where students are able to improve their product in response to comments made by assessors, whether peer or teacher. This can involve several rewrites or presentations, but grading is not finalised until the students indicate the end of revision or until the end of the course. The purposes of such assessment are to maintain a dialogue between assessors and assessee over the criteria for judgment and, in so doing, keep the mathematics and related concepts within the discourse of future activities. Thus, a recursive aspect of learning becomes central to students' classroom experience, enabling the benefits of reflection and the tying-in of later experiences to enhance the sense making of earlier experiences for an 'improved' outcome or grade. This does not imply that the teacher or peers 'work' on students until they think in the same way. Rather, the goal is to encourage students to be effective in presenting their theories.

The Students and Participant-Researchers

The Grade 8 mathematics class in the study consisted of mathematically able students as judged by the feeder elementary schools. (In Western Australia, Grades 1-7 comprise the elementary school, while Grades 8-12 make up the high school). The mathematics courses chosen for these students assume that students are able to continue the Grade 8 phase of the State-mandated K-10 mathematics curriculum without revision components. The Grade 8 course combined the topics of number, function, measurement, and space and inference, and included investigations, problem solving, puzzle work, games and projects.

The other researchers in the team had developed an earlier version of the CLES (Taylor & Fraser, 1991) and were interested in utilising this study to trial the new version. One of them adopted the role of participant-observer and visited the class for the duration of the Egg Project. During lessons, he observed whole-class sessions and inquired into students' activities while they worked in small groups both inside and outside the classroom. He recorded his observations in the form of field notes, conducted after-lesson discussions with the teacher, and interviewed selected groups of students on completion of the project.

Attitude Scale

For purposes of establishing the concurrent validity of the five CLES scales, we included a sixth scale to assess students' attitudes towards their mathematics class. We expected that favourable perceptions of the classroom learning environment would be related to favourable attitudes towards the class. The Attitude scale comprised items that asked students about their anticipation of the class, their sense of the worthwhileness of the class, and the impact of the class on their interest, enjoyment and understanding. The attitude scale was based partly on items in the Test of Science Related Attitudes (TUSRA; Fraser, 1981).

Administration of the CLES

At the mid-point of the five-week Egg Project (i.e., after completion of nine lessons), Loren requested the class to complete the 40-item revised version of the CLES. This timing was chosen because it seemed that a relatively stable classroom environment had been established. Loren explained to the class that the purpose of the activity was to help us trial a questionnaire that we had designed to assist teachers to obtain a better understanding of their students and, consequently, develop more effective teaching approaches. In this way, we attempted to make students feel that they were participating in a research activity that aimed to improve the quality of teaching and learning.

Although we wanted to identify individual student responses for the purpose of conducting follow-up interviews, we were mindful of the need to ensure the integrity of students' responses. To ensure that students felt free to express their genuine opinions we offered them a choice of writing on the questionnaires either their own name or a fictitious name of the group with which they had worked during the project. As a result, eight groups were identified whose membership ranged from two to six students, In addition, there were two students who had appeared to work individually in class.

STATISTICAL ANALYSIS OF CLES RESPONSES

In this section, we discuss first the results of the initial statistical analysis of students' responses to the CLES. On the basis of these results, we selected students for interviews. The selection criteria and the interviewing process are subsequently discussed.

The revised CLES has a 5-point Likert-type frequency response scale which comprises the categories: almost always (5 points), often (4), sometimes (3) seldom (2), and almost never (1). Therefore, the maximum possible mean score of each 8-item scale was 40 and the minimum possible scale mean score was 8 . This response scale was designed to enable students to indicate their perceptions of the frequency of occurrence of a range of salient phenomena (see earlier scale descriptions).

The student responses (N=34) to the questionnaire were analysed statistically to obtain mean scores and standard deviations. As well, estimates of the internal consistency of scales were generated by calculating (1) Cronbach alpha reliability coefficients, (2) item-scale correlation coefficients for each item in relation to both its own scale and other scales, and (3) a scale intercorrelation matrix. Tables 2 to 5 present descriptive scale statistics which indicate, from a psychometric perspective, several problematic aspects of the instrument.

In Table 2, the relatively large standard deviation of most scale mean scores suggests a lack of homogeneity amongst the perceptions of the class. The table shows also that two scales have relatively low internal consistencies (Student Negotiation, a=0.68; Mathematical Uncertainty, a=0.54). The apparent lack of internal inconsistency was a focus of our subsequent investigations.

Table 2

Descriptive Statistics for CLES (N=34)

CLES Scale Mean Standard Alpha

Deviation Coefficient

Personal Relevance 26.2 5.5 0.81

Student Negotiation 28.5 4.1 0.68

Shared Control 20.5 5.5 0.85

Critical Voice 29.9 5.3 0.79

Mathematical Uncertainty 24.3 3.7 0.54

Maximum possible score = 40;

Minimum possible score = 8

Table 3

CLES Items with Low or Negative Item-Scale Correlation Coefficients (N=34)

Scale Item Wording Item-Scale

(In this class. . . ) Correlation

Coefficient

Student I have no interest in other students' ideas. 0.07

Negotiation

Critical Voice I 'put up' with things that prevent me -0.23

from learning.

Mathematical I learn that mathematics provides -0.01

Uncertainty perfect answers to problems.

Mathematics is about using rules to find -0.33

correct answers.

Table 3 shows the four (negatively-worded) items that appeared to make either little contribution or a negative contribution to their respective scales.

We were interested in exploring the relationship between students' attitudes towards the Egg Project and their learning environment perceptions. Table 4 shows the results of calculating a scale intercorrelation matrix . It is apparent that a positive relationship exists between students' attitudes and their perceptions of the learning environment. This relationship is strongest for the three scales of Personal Relevance (r=0.55), Student Negotiation (r=0.49) and Shared Control (r=0.42). These relationships were explored for each of the small groups of students and are discussed below. Table 4 shows also that, in this study, several CLES scales have high degrees of intercorrelation: Personal Relevance and Mathematical Uncertainty (r=0.53), Shared Control and Critical Voice (r=0.63), and Student Negotiation and Critical Voice (r=0.48). Traditionally, learning environment researchers have attempted to minimise the intercorrelation of scales (by rejecting items with unsuitable item-scale correlation coefficients) in order to ensure that each scale represents a relatively unique construct (or factor).

Table 4

Intercorrelations Between Scores of CLES and Attitude Scales (N=34)

Correlation

Scale Student Shared Critical Mathematical Attitude

Negotiation Control Voice Uncertainty

Personal Relevance 0.39 0.16 0.19 0.53 0.55

Student Negotiation - 0.38 0.48 0.09 0.49

Shared Control - - 0.63 0.35 0.42

Critical Voice - - - 0.32 0.33

Mathematical Uncertainty - - - - 0.26

We decided to investigate the source of some of the main statistical problems that are evident in Tables 2 to 4 by inquiring qualitatively into students' responses to the CLES. But first we needed to identify salient students.

We conducted a further analysis of students' CLES responses by examining the scores of each student. Table 5 shows the mean scores of each student group (A - J) for each of the five scales of the CLES as well as for the additional attitude scale. Also shown in Table 5 are the size and sex of each group, and Loren's rating of the relative achievement of the groups based on grades awarded to their interim project reports.

From Table 5, the heterogeneity of classroom learning environment perceptions amongst the student groups — a characteristic that usually is masked by analyses based on the whole class — is evident. For example, for the Shared Control scale, the standard deviation values amongst the 10 student groups cover a large range (Group A SD=9.8; Group C SD=2.6). This result implies that there was a heterogeneity of perceptions within small groups of students and that individual students, therefore, were likely to have had experiences of the classroom that are different from those of other students. Only by examining the perceptions of individual students will researchers be able to understand the nature of this diversity. This level of research was mostly beyond the scope of the study presented in this paper. Apart from one of the students who seemed to work individually, we investigated the perceptions of small groups. Also, it is interesting to note the wide range of attitudes towards the project amongst the class (see Attitude scale). Our interpretive analyses of the interview data are reported and discussed in the next section.

Table 5

Student Group Characteristics and Descriptive Statistics (N=10)

Mean Scale Score (Standard Deviation)
Group ID Size		Sex	Relative Achvment	Attitude	Personal Relevance	Student Negotiation	Shared Control	Critical Voice		Mathematic Uncertainty
A^*	4	F	Hi	21.5 (6.1)	21.8 (3.8)	28.3 (2.8)	20.0 (9.8)	30.0 (8.8)		23.0 (2.6)
B^*	4	F	Hi	27.8 (4.3)	30.0 (4.8)	28.3 (3.6)	20.5 (3.9)	31.8 (7.5)	26.8 (1.3)
C^*	4	M	Av	20.5 (5.1)	20.5 (5.3)	23.3 (2.6)	19.3 (2.6)	25.3 (5.1)	23.0 (1.4)
D^*	3	M	Av	33.0 (0.0)	32.0 (2.0)	32.7 (4.0)	19.3 (6.0)	30.3 (4.5)	23.3 (6.7)
E	4	-		29.3 (2.2)	32.8 (2.9)	29.5 (4.1)	18.3 (4.1)	29.3 (3.9)	27.8 (2.6)
F	6	-		29.5 (5.8)	25.5 (5.2)	31.2 (2.4)	22.7 (7.3)	32.2 (4.7)	23.5 (5.3)
G	2	-		33.5 (6.4)	23.5 (0.7)	31.0 (1.4)	25.5 (0.71)	28.0 (2.8)	20.0 (0.0)
H	1	-		39.0 (2.0)	25.0 (0.0)	27.0 (0.0)	24.0 (0.0)	35.0 (0.0)	28.0 (0.0)
I^*	1	M	Hi	34.0 (0.0)	32.0 (0.0)	32.0 (0.0)	24.0 (0.0)	34.0 (0.0)	26.0 (0.0)
J^*	5	F	Low	25.2 (2.4)	23.6 (1.1)	25.2 (3.9)	18.4 (5.0)	28.4 (2.7)	24.0 (2.0)

^*Groups selected for interview Maximum possible score = 40 Minimum possible score = 8

INTERPRETIVE ANALYSES: RESULTS AND DISCUSSION

Because we wanted to interview a diverse range of students, we chose groups for interview according to a combination of three main criteria. The first was the group's relative achievement in the Egg Project, as indicated by the interim grade given to project reports; we wanted to interview both high and low achievers. The second criterion was the group's attitude towards the project; we wanted to interview students who had more favourable and less favourable attitudes. The third criterion was the sex of the students; we wanted both sexes to be represented. Table 5 summarises the characteristics of the six student groups which participated in the interviews, and Figure 1 shows graphically the distribution of the mean scale scores of their responses to the CLES.

The Interviews

Each group of students was interviewed for about 30 minutes. A vacant classroom at the school was used, and students sat in a semi-circle with the interviewer. Their approval for audio-recording was obtained after ensuring them of the confidentiality of their responses (especially in relation to the teacher). Transcripts of interviews were a major source of data for this paper.

A semi-structured interview was used which comprised the following three-step format. Firstly, students' thinking was focussed on the Egg Project by asking them about its in the context of the mathematics learning environment that they had experienced throughout the year. Secondly, students were asked about their retrospective perceptions of the Egg Project. In particular, they were asked to explain apparent differences between their current responses (i.e., during the interview) and their past responses to the CLES. To assist with the comparison, each student was given the copy of the CLES that they had completed in class several weeks previously. Thirdly, more detailed explanations were sought about students' perceptions in relation to key issues by focussing them on specific items in the CLES.

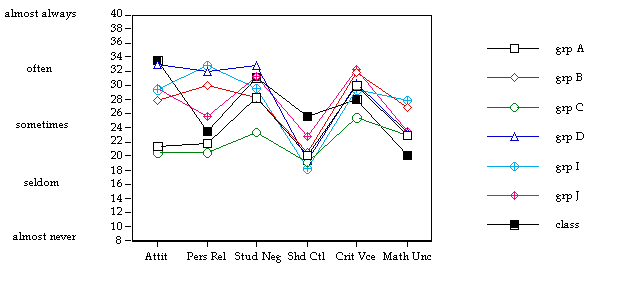
Fig 1. Distribution of scale mean scores of interviewed groups & whole class (N=7)

Interpretive Data Analyses and Assertions

The following results are based on data generated largely from student interviews, classroom observations, and the administration of the CLES to a class of 34 students. The results are presented in the form of three assertions (Erickson, 1986) which constitute emergent theory that has a sound empirical base.

1. ASSERTION 1. In the context of high school mathematics classrooms that are undergoing a constructivist transformation, the five CLES scales — Personal Relevance, Student Negotiation, Shared Control, Critical Voice, Uncertainty — have the capacity to contribute to a plausible account of the classroom learning environment.

2. ASSERTION 2. The capacity of the CLES to contribute to a plausible account of a classroom learning environment might be optimised by careful design that: (1) avoids conceptually asymmetric and conceptually complex items, and (2) counters students' tendency to adopt alternative experiential contexts as referents when responding to items.

3. ASSERTION 3. When determining the practical viability of learning environment questionnaires, especially in the context of classroom learning environments undergoing transformation, anomalies which arise from statistical analyses can be investigated profitably by interpretive inquiry.

Evidence that warrants the three assertions is presented in the following sections which constitute an interpretive account of the statistical analyses of the revised CLES .

Personal Relevance

According to the CLES data, during the 9-lesson period preceding the administration of the CLES, the class as a whole perceived the Egg Project to be relevant to the world outside of school only sometimes (see Table 1, mean=26.2, SD=5.5). However, group perceptions ranged from relevant often to relevant infrequently (see Table 4, 21.5<mean<39.0). The data indicate also that students with more favourable attitudes tended to perceive the project as being relevant more frequently than did students with less favourable attitudes (see Table 3: r=0.55).

When we interviewed students with the least favourable attitudes (Groups A, C), we found that these students perceived the project to have no apparent relevance during the early weeks:

S3(A) It seemed stupid to find the surface area of an egg. . . We were frustrated that it was an egg. . . The actual idea's still pretty silly.

S1(C) I thought it was a bit of a waste of time . . . The results weren't so beneficial for us. . . You just learned a bit of problem solving group work. . . . I don't know how we can turn this project into other things in life.

S2(C) [L]earning the surface area of an egg doesn't mean anything really.

Similarly, students with slightly more favourable attitudes (Groups B, J) reported a lack of awareness of the general relevance of the project:

S1(B) [W]e didn't know why we were doing it. . . . It was boring. . . . Who wants to know the surface area of an egg? Eat it, then chuck it away!

S2(B) It got really exciting towards the end, but it was boring at the beginning.

S1(J) I thought it was pretty well a waste of time. . . . In 7 or 8 years, I don't think it's really going to help us.

This is not a surprising result in view of the Loren's stated goals of the project. According to observational data, Loren had introduced the project to the class in the school mathematics context of work previously completed on the concept of area and use of scattergraphs for representing data and identifying relationships between variables. He had explained the purpose of the project as an empirical investigation of the surface area of an egg that would make use of data to be pooled from all groups. During the next 8 lessons, Loren's brief explanations to the class of the goals of the project referred mostly to issues such as data collection and analysis, "experimenting like science" (Field notes, Lesson 5), and "real genuine mathematical thinking" (Field notes, Lesson 9), but made little mention of the relevance of the project to the world outside of school.

So, how can we account for the CLES data that indicate high degrees of perceived relevance of the project amongst some students (Figure 1: Groups I, D)? Interestingly, the CLES data indicate also that these students had the most favourable attitudes amongst the class. When we interviewed these students, we found that they explained the relevance of the project to the world outside of school in terms of their imagined future careers or the opportunity provided by the project to learn how to work collaboratively and conduct investigations:

S1(D) [I]f we go into a job like engineering or something we need to know how to figure out things like this.

S3(D) [G]roup work. . . working together using all the brains that there were.

S1(I) [Y[You might have to do some investigative work. . . and the egg thing's just something to help you on the way.

Changing Experiential Contexts

It therefore seemed that when responding to the CLES items, a minority of students (with more positive attitudes) seemed to transcend the immediate experiential context of the project (i.e., experiences of finding the surface area of an egg) and referred to imagined experiential contexts (e.g., future careers) in which the learning processes of the project (i.e., figuring things out, investigating, cooperating) had a high degree of perceived relevance. By contrast, the majority of students (with less favourable attitudes) tended to respond to the CLES items within the immediate experiential context of the project. It seems that, in the absence of any explicit indication by the teacher of the relevance of the project beyond its stated school mathematics goals, students' perceptions of the project's relevance were dependent on their a priori beliefs, values and imaginations. The problem of changing experiential contexts is explored in greater detail in relation to the results for the Uncertainty scale.

We conclude that the Personal Relevance scale of the CLES generated data about students' perceptions that generally were congruent with data from observations and interviews. The apparently anomalous higher-than-expected perceptions of personal relevance indicated by a minority of students seem to have resulted from an absence of direct instruction about the relevance of the project to the world outside of school.

Recommendation 1

Future research is necessary to determine the extent to which the Personal Relevance scale is able to provide a plausible account of learning environments in which students have extensive opportunities to develop understandings of the relevance of their mathematical activities to the world outside of school.

Explanatory Teacher Note

The issue of relevance of mathematics had been an ongoing part of discussions in the classroom since the first lesson on the Egg Project. The students found much of the mathematics was not relevant to their daily life activities, particularly outside the school context of successfully completing studies. However, this did not deter him from continuing to discuss the relevance issue although much of the discussion regarding the relevance about finding surface areas of solids occurred in earlier topics which dealt with surface areas of Euclidean shapes such as cubes and spheres. There is not much to discuss. Even less so about the need, in practice, to find the surface area of eggs, although he did draw an analogy to some mathematical work that he had done for a friend. This work aimed to establish a reasonable formula for finding the surface area and volume of human testicles from ultrasound pictures for his research on male sterility. So, Loren chose to tell the class his reasons for setting the project.

It appeared to Loren that many students considered the large assessment component as giving relevance to the project, especially as most students regarded the project as an opportunity to get a high score. For other students, the project looked like fun and therefore seemed relevant. The perceived relevance of the project is also something that can be judged positively by the students at some future time if the current experience proves to be useful. Choosing a project or activity for students with this in mind is very much a part of teaching.

Student Negotiation

The CLES data indicate that, during the early weeks of the Egg Project, the class as a whole perceived that students negotiated with each other relatively frequently (see Table 1, mean=28.5, sd=4.1). Group perceptions of the frequency with which they negotiated with other students ranged from sometimes to often (see Table 4, 23.3<mean<32.7). Figure 1 indicates that, with one exception, students with more favourable attitudes tended to perceive themselves as negotiating with other students more frequently than did students with less favourable attitudes (see Table 3: r=0.49). The exceptional students belonged to Group A (high achieving girls) who, despite their unfavourable attitudes, indicated that they negotiated frequently within their group.

During classroom observations, it was evident that, for most lessons, most students discussed their work with other students in their group and, occasionally, with students from other groups, especially during times when groups were seeking data from other groups. However, we found it rather difficult to observe group discussions for the purpose of determining the nature of their discourse. When we approached groups, they tended to stop their discussions and direct their attention to us. Nevertheless, brief observations indicated that students seemed to be explaining their ideas to their group (e.g., about data collection methods) and deciding which ideas were worth testing. When we interviewed students with the strongest perceptions of negotiation (Groups D, A), they explained that they had spent a considerable amount of time in class considering each other's ideas carefully:

Intvr For how much of the time were you thinking seriously about the other person's ideas?

S1(A) Half the time.

S2(A) A lot of the time. What we do is just put in our ideas.

S3(A) We were talking a lot, but it was about the project.

S2(A) We were debating which ideas were good and which ideas, you know, we didn't need.

S1(D) A couple of times we had different methods of measuring, and we had to figure out which one to use and which one was the best.

S2(D) And we tried the ideas over and over with lots and lots of eggs. Then we just finally negotiated. . . what should be the best one. . . In group work, if you're working on a really tough problem like [the Egg Project], I think you need. . . coordination. . . because. . . you need a lot of people to help you, not just one person.

During classroom observations, it also was evident that, within other groups, students were working individually after having agreed about a division of labour in relation to a range of complementary tasks (e.g., taking measurements, compiling tables of data, report writing). Very little discussion of ideas was evident. Interviews with students who perceived themselves as engaged in negotiations less frequently confirmed these observations:

S1(C) We were pretty low on [negotiations].

S2(C) We each had a bit to do.

S1(C) Yes. We did our own job and that was probably it.

S1(J) Alice [pseudonym] did most of. . . the graphs.

S2(J) She wrote it all up.

S1(J) I wrote it all up. . . how we did it.

S2(J) I sort of did the graphs and that while she was writing.

Interestingly, the CLES data of the high achieving male student who had been observed to be working independently indicated a high degree of negotiation with other students (Figure 1: Group I). This apparent anomaly puzzled us. However, during the interview, the student explained that, although he rarely initiated discussions with other students (probably because of his shyness), he often listened carefully to other students' explanations and often explained his ideas to other students when they consulted him. It seems, therefore, that fruitful negotiation can occur amongst students who apparently are working independently, especially if the classroom environment provides opportunities for students to move around and consult one another.

Conceptual Complexity

Several items in the Student Negotiation scale elicited inconsistent responses which resulted in less-than-satisfactory item-scale correlation coefficients (see Table 2) and contributed to a relatively low alpha reliability coefficient for the scale as a whole (see Table 1, a=0.68). Two of the items are negatively worded (Items 41, 47) which is a feature that might have given rise to interpretation difficulties when students were considering a suitable category from the frequency response scale. For example, to choose seldom or almost never (as did a total of 25 students in this study) as a response to Item 41 (I have no interest in other students ideas), requires students to think in terms of a conceptually complex double negative statement that has a greater likelihood of being interpreted inconsistently than do items that are positively worded.

Recommendation 2

We feel that learning environment questionnaires should avoid negatively-worded items that are likely to be conceptually complex. Consequently, when refining the CLES scales, we rejected Item 41, and changed Item 47 into a positively-worded form: Other students pay attention to my ideas.

In relation to the Student Negotiation scale of the CLES , we concluded that the data generally yielded a plausible account of the classroom learning environment that is consistent with data from other sources.

Recommendation 3

However, because students received little direct instruction on how to organise their groups to optimise student negotiations, we feel that further research is needed to determine the efficacy of this scale for generating plausible accounts of classroom learning environments in which students have extensive opportunities to engage in rich negotiations with one another.

Explanatory Teacher Note

It was intentional on Loren's part not to organise and structure the groups and their roles. He felt that it was not his role to guess the most appropriate configuration to get the best results. Rather, he believed that this was part of the problem solving aspect of the project.

Shared Control

The CLES data for the Shared Control scale indicate that, as a whole, the class perceived that relatively infrequently they shared control with the teacher of the management of the classroom learning environment (see Table 1: mean=20.5, sd=5.5). In general, students perceived that less than sometimes were they able to help the teacher plan the learning activities (Item 4), and have a say in deciding what activities to do and how much time to spend on an activity (Items 40, 22, respectively).

During the interviews, one of our chief concerns was to minimise the amount of lesson time forfeited by students. We did this by focussing on the extent to which students perceived that they had had a say, in a general sense, in what to do in relation to their participation in the Egg Project. We found that, regardless of their attitudes or levels of achievement, and with one exception, students indicated that they had had very little say in shaping the project's activities. Whereas most interviewed students acknowledged a degree of control over their learning activities on a moment-by-moment basis (e.g., negotiating with each other about empirical methods), they seemed to believe that the locus of control of the general management of the early part of the project lied almost entirely with the teacher.

Intvr Do you reckon the teacher gave you much say in making decisions and deciding what to do?

S3(A) He gave us three sheets, and said what we had to do during the project.

S2(A) It was sort of really laid out, what we had to do.

S3(A) Yes, we had to do this, this and this. And we couldn't change that in any way. We had to do it THAT way and hand it in THAT way!

S1(B) [The teacher] told us what was asked of us. . . and that's all we did.

S1(C) He just basically told us what to do, and we just tried to do it. . . just [to] give him a result.

Nevertheless, the stark contrast with earlier classroom experiences of working out of textbooks was sufficient to cause the highest achieving student (Group I) to celebrate the increase in control that he had experienced sometimes during the project:

Intvr You think that the teacher doesn't give you much say in what to do in the class. Would that be true?

S1(I) Yes, I suppose, because. . . we do textbooks. You just learn out of it. You can't choose what you want to do.

Intvr And in the Egg Project, did you feel the same?

S1(I) Not really, because you can do it - get the information - however you like. . . . You had to do the Egg Project, but you could do it how you liked!

Observational data were highly consistent with students' recorded perceptions. During the nine-lesson period prior to the administration of the CLES, we observed students exercising a limited degree of autonomy with respect to their participation in the management of the classroom learning environment. Generally, students exercised most control over the practical problem-solving component of their learning activities. During these activities, which occupied most of the lesson time, students shared control with other students in their group (i.e., designing data collection methods, recording data). However, the overall goal of the project — "to find a simple way to estimate the surface area of an egg" — was prescribed by Loren. As the lessons proceeded, Loren prescribed also the data to be collected (i.e., which variables to measure) and the types of analysis (i.e., which relationships between variables were of interest). Because of the Loren's goal of pooling group data and comparing the results of each group's data analyses, students were given little opportunity to develop learning goals that differed from the teacher's goals.

As well, the nature of the formal assessment of the project was prescribed by the teacher. Groups were directed to submit a single written report that addressed a set of criteria determined by the teacher. The CLES data (for Items 10, 34, 46) indicate that students perceived themselves as having infrequent opportunities to participate with the teacher in assessing their learning. In general, data from all sources confirmed that students were provided with limited opportunities to share with the teacher control of their participation in the project.

In this study, the Shared Control scale had a satisfactory internal consistency (see Table 1: a=0.85). An analysis of individual items indicated that only a single item (Item 28: I have control over my learning) had a relatively small item-scale correlation coefficient (r=0.36). The item elicited an overall response that indicated that students perceived themselves to have frequent control over their learning (i.e., more than sometimes). We attributed this anomalous result to the less than precise nature of the term control which might have been interpreted in relation to students' collaborative decision making rather than in relation to sharing control with the teacher. Item-scale correlations indicate that it had a strong positive association with three other scales.

Recommendation 4

When designing an item, care should be taken to avoid the use of terms that might give rise to a range of interpretations at variance with the intention of its own scale. In the case of Item 28, we rejected it from the instrument.

We concluded that the Shared Control data yielded a plausible account of students' classroom learning environment perceptions that was consistent with data from interviews, classroom observations and documentation.

Recommendation 5

However, further research is needed to determine the extent to which this scale generates a plausible account of classroom learning environments that offer extensive opportunities for students to exercise autonomy in relation to the design and management of their own learning activities.

Explanatory Teacher Note

Constraints were operating in the planning and execution of the Egg Project. For Loren, the project's form had to be perceived by multiple audiences — colleagues, students, parents and school administration — as 'fitting in' with the overall curriculum. The topic choice and aspects of the implementation were consequences of a demand to justify its presence in the course, and the production of a suitable assessment product within a time limit for reporting purposes. The students had strong views about what should happen in a mathematics classroom, including the teacher doing a lot of the directing. The students were very aware of what their colleagues were experiencing in other classes covering the same mathematics course. There was not a lot of scope to allow students to negotiate the project topic or initial guidelines. Furthermore, it was evident that, from the start of the Egg Project, students treated the challenge differently. For some students, it was a chance to take things easy and rely on other groups to set the pace; some tried to get the answers from Loren; and some required regular reassurance from him that they were capable of solving the problem. Often, Loren felt that students were playing a game to short-cut the project and meet their own goals, whatever they might have been. At the time, Loren was a little frustrated with these games and, consequently, was blunt with students. However, he remained confident that they would have more appreciation of the project as they made progress.

Critical Voice

Although students shared with the teacher little control over their participation in the Egg Project, they were not reluctant to express their opinions to the teacher about issues of importance to them. The CLES data in Table 1 indicate that the class, as a whole, believed that it was legitimate to exercise frequently a critical voice about the quality of their learning activities (mean=29.9, sd=5.3). Students' perceptions of the extent to which opportunities existed to question the teacher's instructional plans and methods and express concerns about any impediments to their learning ranged from sometimes to more than often (see Table 4: 25.3<mean<35.0). Not surprisingly, perhaps, the highest achieving students (Groups A, B, I) indicated that they felt most empowered in this respect (see Figure 1).

The interview focussed on the extent to which students experienced opportunities to be critical, in a general sense, about the project. During interviews with students who were amongst those who achieved the highest grades for their project reports, it was apparent that students felt themselves to be sufficiently empowered to approach the teacher with their complaints or felt that they could do so if they wished. Most notable was the group of high achieving female students which had had relatively unfavourable attitudes during the initial 9-lesson period (Group A):

Intvr Often you thought that you had a critical voice?

S1(A) Yes!

S3(A) Arguing!

S2(A) With Mr White. A lot!

Intvr Did you feel free to complain to Mr White?

S1(A) Yes. . . a lot.

S2(A) Definitely. . . . I think he got pretty high blood pressure from us.

S1(B) Yes. . . . We wouldn't be afraid to go up to Mr White and say "We don't like this", or "We don't understand this".

S2(B) Or "This doesn't look right, can you help us".

Intvr You felt that you had the opportunity to express your feelings, to complain if you wanted to, to say that you didn't like something?

S1(B) Or even if, like, he just said that "I'm not going to change it. Go back to your seat", we still wouldn't mind going up there.

S1(I) I just think that I can if I want to.

By contrast, students who had achieved relatively low grades for their project reports (and who had less favourable attitudes) seemed not to feel sufficiently empowered to exercise a critical voice. There are indications in the following interview excerpts that disempowerment was associated with students' awe of the teacher's authority (Group C) and with students' chronic resignation that mathematics seldom seemed to be of direct relevance to the world outside of school (Group J):

Intvr You didn't express your opinion about the fact that you didn't like doing [the project] much?

S1(C) No. . . . Because it was the whole class that was doing [the project].

S2(C) No. He's the teacher, you know. . . . If he wants us to do a project we'll do the project. . . or else we'll get bad marks.

Intvr Did you let the teacher know that you didn't think that the project was particularly relevant?

S2(J) Yes, but not properly. . . not seriously.

Intvr You were just joking around with him, were you?

S1(J) Yes.

S2(J) Sort of like saying we don't want to do it.

Intvr OK. Why would you have not told him seriously?

S2(J) We didn't mind really, doing the project.

Intvr You didn't mind that it wasn't all that relevant to the outside world?

S1(J) No.

Intvr Is mathematics usually like that?

S1(J) Yes.

Classroom observations indicated that students who exercised a critical voice with the teacher did so largely in private, rather than during whole-class interactions.

Explanatory Teacher Note

For one particular student in this class (Group I), 20 weeks into the school year was the first time when, in his view, he had actually challenged the teacher to argue for a different outcome. After seven-and-a-half years of schooling, this was a big step for him, and he considered that he had exercised often a critical voice. Not so for one of the girls (Group A) who challenged Loren's decisions almost every lesson.

Mathematical Uncertainty

The CLES data in Table 1 indicate that, during the initial nine-lesson period, the class as a whole had experienced mathematics as a fallible human activity only some of the time (mean=24.3, sd=3.7). A small correlation (see Table 3: r=0.26) between the attitude and mathematical uncertainty scale scores indicates that, in this study, students' attitudes were not strongly related to their experiences of mathematical uncertainty.

Of great concern to us were the statistical data in Table 2 that indicate the unsuitability of several key items with unsatisfactory item-scale correlation coefficients (Item 38, r=-0.01; Item 44, r=-0.33). Normally, such items would be rejected in favour of items that made a greater contribution to their scale (i.e., r>0.30). However, because of our interest in the educational significance of the items, we were reluctant to abandon them on purely statistical grounds, and decided to investigate students' responses to them. Our investigations yielded valuable insights into the nature of a changing learning environment.

Changing Experiential Contexts

First we focussed on Item 38 — I learn that mathematics provides perfect answers to problems. During interviews, we asked students about their experiences of using mathematics to obtain a perfect answer to the Egg Project goal of finding a rule for the surface area of an egg. Of the six groups of students who were interviewed, Group B (one of the highest achieving female groups with a favourable attitude towards the Egg Project) reported an insightful experience of mathematical uncertainty.

Although they were somewhat unsure of their ideas during the interview, there was a recognition among them of the imperfect nature of the rule that they were trying to invent, especially in contrast to the well-known numerical rules (or axioms) that they used in other contexts. They attributed this lack of mathematical certainty to the irregularity (i.e., non-Euclidean nature) of the actual (real world) eggs that they were using and to the consequent difficulty of modelling the shape mathematically:

Intvr Was it possible to find a perfect answer in the Egg Project?

S3(B) I think . . . there probably would have been.

S1(B) I don't think. . . I don't know.

S2(B) I don't think there is an actual formula for the surface area of an egg. You could find the volume, probably, like with those [measuring] cylinders. And you could actually find the width [i.e., girth] with the Vernier callipers. But like you couldn't actually do the main question which was asked.

Intvr OK. Do you [inviting another student] think that was the case?

S3(B) Yes, because isn't the egg shaped, or something, inside the chicken . . . before it comes out? So, that way, the egg isn't an exact shape. I mean it could be a different type of shape.

Intvr But in other mathematics do you think you were able to find perfect answers?

S2(B) Well, in most things, like when it was like sums and that, we were given numbers and you had to get the perfect answer.

In contrast to their stated frequent experience of mathematical uncertainty in relation to achieving the main goal of the Egg Project, these students had indicated in their responses to the CLES that they had only sometimes or seldom learned that mathematics provides perfect answers to problems. We wondered how this apparent anomaly could be explained. The interview helped to provide a plausible explanation. When responding to the CLES , these students acknowledged that they had changed the context within which they were thinking about their mathematics learning experiences. They had adopted as the main referent the context of their more familiar learning experiences of mathematical certainty which tended to subsume and to render much less significant the tentative experiences of mathematical uncertainty that were occurring during the Egg Project. As a result, their CLES responses understated the frequency of their experience of mathematical uncertainty:

Intvr Item 38: I learned that maths provides perfect answers to problems. What have you got there?

S2(B) Sometimes.

S3(B) Seldom.

S1(B) Sometimes.

Intvr And during the Egg Project, did you have evidence that that was the case?

S2(B) No, we never had perfect answers. . . but in other maths there's always like a perfect answer.

S1(B) Yes, but in other maths you do. . . . So, I think that's probably why I put sometimes.

The tendency to change experiential contexts when responding to CLES items was very evident in the final comments of one of the students who had been reflecting on my questions and who volunteered the explanation that, when responding to the CLES items:

S1(B) I started off using the Egg Project. Then I, sort of, moved over to maths overall.

Intvr When you were answering the questionnaire?

S1(B) Yes. I sort of stopped and then went to maths overall.

In relation to our second statistically problematic item (see Table 2: Item 44, r=-0.33), there is evidence that students had changed the context of their thinking when responding to this negatively-worded item. Although student I (the high achieving male student with the highly favourable attitude) claimed to have had frequent experience of the activity of rule invention, when responding to Item 44 he seems to have used as the main referent his predominant experience of using mathematical rules (this issue is developed further in the section on conceptual asymmetry of negatively-worded items). As a result, his CLES response understated his experience of mathematical uncertainty:

Intvr Item 44: Maths is about using rules to find correct answers. What did you have there?

S1(I) Almost always.

Intvr Do you think maths is about inventing rules, or using rules, or both?

S1(I) Both.

Intvr Were you doing any invention this year?

S1(I) No.

Intvr What about the Egg Project? Was that an invention exercise?

S1(I) Yes, you had to find a formula. So, that's inventing.

Intvr A formula that wasn't known before?

S1(I) Yes.

Another example of students changing their experiential contexts when responding to this item, and consequently understating their experiences of mathematical uncertainty, was obtained from the Group B students:

Intvr Item 44: Maths is about using rules to find correct answers. What have you got for that?

S2(B) Often.

S3(B) Often.

Intvr When you answered the question were you thinking about the Egg Project, or were you thinking about maths outside of the Egg Project?

S3(B) Maths outside.

S2(B) I was thinking about maths outside, like 'length times width', or whatever.

What was the influence on the Uncertainty scale statistics of students changing the contexts of their thinking about their mathematics learning experiences when responding to items? At this stage, it is impossible to give a comprehensive account because we do not have sufficient data for all items on this emergent research question. However, in relation to our two statistically problematic items (Items 38, 44), two important consequences have been identified.

First, because students understated the frequency of their experiences of mathematical uncertainty during the Egg Project when responding to these items, the overall scale mean score (see Table 1: mean=24.3) was depressed. Second, as a result of averaging their experiences of different learning environments, students tended to choose the mid-range response of sometimes. When analysed statistically, the variance in the scores of students' responses was relatively small, especially for Item 44 (sd=0.68). Consequently, the values of the item-scale correlation coefficients of these items also were relatively small.

So, why did students change the context of their experiences when responding to items in the Uncertainty scale? We believe that one of the main reasons concerns the novelty of students' experiences of sustained mathematical uncertainty and their tentativeness in accepting the authenticity of a counter-intuitive experience of a constructivist epistemology. The tendency amongst the class to attribute greater authenticity to their familiar prior experiences of the certainty of mathematics might have been strengthened by their perception that mathematical uncertainty did not seem to be a legitimate learning goal. Classroom observations indicate that, apart from stating the overall goal of the project — to find a general formula for the surface area of an egg — Loren made little attempt to establish mathematical uncertainty explicitly as a learning goal for the class.

In a state of intellectual and emotional uncertainty about the legitimacy of their new experiences during the Egg Project students, therefore, might have responded to items of the Uncertainty scale by using as a referent their rich experiences in more traditional learning environments whose legitimacy was beyond doubt.

Recommendation 6

In order to determine the extent to which items in the Uncertainty scale can elicit dependable responses, it is necessary to trial the CLES in a classroom learning environment that provides rich and sustained experiences of mathematical uncertainty whose legitimacy as a learning goal has been affirmed by the teacher.

Explanatory Teacher Note

From the first day of the school year, Loren had endeavoured to have uncertainty of mathematics as part of the classroom discourse. Counting, symbols, conventions, concepts and ideals had been discussed in terms of subjective decisions being made on the bases of other beliefs, preferences, and desires such as uniformity, simplification, universalism or religion (e.g., positive indicated to the right, negative to the left). Non-routine puzzles and problems had been part of the class program leading up to the Egg Project. Many problems provided multiple solutions and needed negotiation for a best answer. The difference with the Egg Project related more to the size of the project, the need for measurements to be made, the negotiation of plausible methods and answers, and assessment. It is not clear to Loren what should be presented to students as demonstrating mathematical uncertainty, other than to give them opportunities to experience framing of problems. That is, to provide opportunities to experience the social construction of mathematics by sorting out information to see if there is a problem and whether the problem can be mathematised, and making a choice of models in which to redescribe the problem. Can a teacher tell a student what uncertainty is, or is it a sense or feeling embodied in experience?

We believe that a contributing factor in students' practice of changing their experiential contexts when responding to items in the Uncertainty scale concerns the nature of the prompt in the CLES. This prompt, which takes the form of In this class. . . and precedes each group of three items, was designed to focus students' thinking on the learning environment in their current class. However, in the case of this study, where a changing and unstable classroom learning environment existed, it seems that the prompt failed to maintain students' new experiences as a referent for responding to items. In the absence of rich experiences amongst students of mathematical uncertainty during the Egg Project, students changed the context of their thinking to their prior learning experiences in this class.

Recommendation 7

In the context of a changing learning environment, questionnaire prompts should be designed to maintain students' thinking on the appropriate set of experiences. For example, in this study an appropriate prompt might have been: During the Egg Project.

Explanatory Teacher Note

Although the CLES was administered during the Egg Project, it did not ask students to confine their considerations to this project. It seems that the students were more likely to respond to each question according to what contexts the questions suggested as being most meaningful. The result could be an aggregate of meanings related to at least the whole year's experiences in Loren's class, rather than to experiences at only the specific point in time when the CLES was administered. Furthermore, although any student can give what appear to be contradictory answers, such contradictions might not exist for the student. Researchers and teachers tend to give more primacy to consistency and logic of student answers, and have a fear of contradictory answers. They tend to regard the context of classroom learning environments as universal, timeless and unchanging, and tend to think that, when students make sense of a new experience in a different way, they update automatically all other related meanings such that contradictions are ironed out.

Conceptual Asymmetry

Our investigation into the statistically problematic Item 44 — Mathematics is about using rules to find correct answers — provided another explanation for its apparently negative contribution to the Uncertainty scale (Table 2: r=-0.33).

During the Egg Project, students made use of their prior mathematical knowledge, especially their knowledge of mathematical rules, to enable them to mathematise the problem of finding a rule for the surface area of an egg. They devised mathematical models of their eggs (e.g., hemispheres, triangular nets), measured various linear dimensions (e.g., width, circumference, girth), and calculated other dimensions (e.g., volume, mass) in order to obtain approximations of the surface areas of their eggs. After pooling their results, the various groups set about the complex task of ordering the data and looking for patterns that might be expressible in the form of a general rule for the surface area of an egg. Clearly, the Egg Project comprised much use of already-known mathematical rules during the process of inventive problem-solving.

The student interview data indicate that most students recognised that the Egg Project was an activity in which they used well-known mathematical rules (e.g., surface area of triangular and spherical shapes; rules of multiplication and addition) in their overall attempts to invent a general mathematical rule for the surface area of an egg.

Intvr Is maths about using rules, or is it about inventing rules? Think about the Egg Project.

S1(A) I think we invented. . .

S2(A) We used [rules] more. We used the 'sphere theory'.

S1(D) I've got "sometimes" because. . . for area and surface area [Euclidean shapes] you can have rules. But for other areas [non-Euclidean shapes] you can't because they just don't work.

Intvr Item 44: Maths is about using rules to find correct answers. Did that apply in the Egg Project?

S1(C) Yes, we used a couple of rules. Like how to find the volume.

S2(C) I used rules like working out the volume by putting it in water.

Intvr And you were saying before that you were trying to invent a new rule. Is that right?

S1(C) Yes, we used a bit of both.

Although students claimed that, in hindsight, they had both used and invented mathematical rules during the Egg Project, when responding to Item 44 of the CLES the more familiar (moment-by-moment) experience of using mathematical rules seems to have dominated their thinking. Only three of the total of 34 students chose a response category (i.e., seldom) that, when reverse-scored, made a positive contribution to the internal consistency of the Uncertainty scale. Students' experience of using rules seems to have overshadowed their experience of inventing a rule. What might be the reason for this outcome?

At the time of responding to the CLES, the experience of having invented a mathematical rule was unfamiliar to the class. Classroom observations revealed that none of the class had achieved the main goal of the project, that is, to invent a general rule for finding the surface area of an egg. Instead of having invented a general rule students were engaged in open-ended processes of invention that did not necessarily guarantee the existence of a general rule. Interviews indicated that: (1) students with unfavourable attitudes towards the project expressed doubts about the existence of a general rule; and (2) the majority of the class seemed to have experienced little sense of personal relevance in relation to the main goal of the project (see Personal Relevance scale). It is not surprising, therefore, that students' responses to Item 44 reflected their dominant experience of using, rather than inventing, mathematical rules.

However, we believe that there is another, more important, issue associated with the problematic nature of Item 44 (using rules). This negatively-worded item was designed on the assumption that, when reverse-scored, it was equivalent to the concept of inventing mathematical rules. That is, we had assumed, somewhat naively, that in a constructivist learning environment students would be engaged to a much greater extent in invention-type activities than in rule-using-type activities. What we learned from the Egg Project was that the two activities are complementary rather than antithetical. In order to invent new mathematical knowledge students must utilise their extant mathematical knowledge, much of which is expressible in the form of rules. What characterises an emergent constructivist learning environment, therefore, is not the abandonment of rule-using activity but a new instructional emphasis on students use of known-rules for the purpose of experiencing mathematical knowledge as an uncertain product of human endeavour. In other words, students would experience not only the usefulness of using mathematical rules to invent models of problematic aspects of their everyday worlds, but also they would experience the inherent uncertainty of the mathematical knowledge that they construct during this process.

As a result of our investigation of Item 44, we concluded that a conceptual asymmetry exists between the item and the Uncertainty scale, and that the item does not serve as a legitimate negatively-worded item. We have realised the importance of not assuming that conceptual symmetry can be achieved readily between a scale and a negatively-worded item, especially where the negatively-worded item addresses experiences that might have a legitimate role in various learning environments including an emergent constructivist environment. Our experience in previous research confirms this concern. For example, in an earlier version of the CLES, an Autonomy scale was designed to obtain measures of the exeunt to which students experienced opportunities to exercise self-control and independence from the teacher. The scale contained a few items that referred to the role of the teacher as an agent of control. It was assumed that, when reverse-scored, these items would be conceptually equivalent to the positively-worded items that referred to the role of students as agents of control. However, factor analysis of responses to these items indicated that they were distinct factors, a result that suggested that the assumption of conceptual equivalence was invalid.

We concluded that, if the CLES is to be of use to teachers in monitoring emergent constructivist learning environments, then it should aim to provide measures of the presence of desired attributes rather than the absence of undesirable or complementary attributes that might characterise alternative learning environments.

Recommendation 8

When designing negatively-worded items, care should be taken to avoid conceptual asymmetry between items and their scales resulting from the inappropriate use of non-equivalent concepts. Therefore, (1) Item 44 should be reworded in the form: I learn that mathematics is about inventing rules, and (2) Item 38 should be reworded in the form: I learn that mathematics cannot provide perfect answers.

Conclusion

This paper presents an analysis of the results of a trial of the revised Constructivist Learning Environment Survey (CLES) that was conducted in a single high school mathematics classroom during 1993. We had chosen that particular classroom because we wanted to assess the efficacy of the CLES in generating a plausible account of a classroom learning environment that was characterised by the presence, rather than absence, of key attributes that were compatible with the critical constructivist perspective underpinning the five CLES scales.

What might have been considered, from a purely psychometric perspective, to be a relatively straightforward task of generating statistical data and refining the CLES scales by abandoning or modifying problematic items became, instead, an intriguing inquiry into the complex nature of a changing classroom learning environment. During this process, we found ourselves supplementing psychometric warrants (e.g., reliability) associated with traditional learning environment questionnaires. We were able to do this by adopting an interpretive research framework within which we studied in detail the complex array of perceptions held by the teacher and students. The statistical analyses, especially problematic results (such as negative item-scale correlation coefficients) became starting points, rather than end points, of our investigation. We sought to generate plausible explanations for anomalies that were apparent in both quantitative and qualitative analyses.

The richness of our investigation was enhanced by the establishment of a dialogical relationship between the teacher-researcher and one of the participant-researchers. The teacher-researcher was able to express his own critical voice about the significance of both the data that were generated in the study and the participant-researchers' interpretations. His voice appears in two ways throughout the paper. The first is his influence (by means of continuous negotiations during the study) on the participant-researchers' interpretations that are presented in the discussion of the results. The second, which is in a more explicit form, is by means of the Explanatory Teacher Notes which are appended to, and provide alternative interpretations of, the participant-researchers' analyses.

One of the outcomes of the study was our realisation of the difficulty faced by teachers who wish to transform their classroom learning environments in accordance with a constructivist philosophy. The process of change might not be a simple transition from state A (e.g., high degrees of teacher control and mathematical certainty) to state B (e.g., high degrees of student autonomy and mathematical uncertainty). Rather, the process might be a complex transformation that involves the partial coexistence of both states, especially where shared attributes are involved. For example, in this study, we came to understand that, whereas state A is concerned mostly with the use of mathematical rules, in state B students both use and invent mathematical rules. In a transformative situation, in which state B is being introduced, a student is likely to hold conflicting beliefs about the nature of his/her experiences, and can tend to use his/her more familiar and secure experiences (e.g., of state A) as a referent when responding to items in a learning environment questionnaire, thereby under-reporting experiences of state B. In this paper, we refer to this practice as students changing their experiential contexts. We suggest that this problem might be minimised by careful design of items (e.g., avoid conceptually asymmetric items) and by careful design of prompts that constrain students' thinking within an appropriate experiential context.

Another important outcome of the study was our realisation of the difficulty facing learning environment researchers who wish to promote the adoption by teachers of the role of teacher-researcher for the purpose of undertaking pedagogical change of a constructivist nature. The CLES comprises five scales that, for many teachers, could represent five radical transformations of their current learning environments. We are sufficiently realistic that we would not wish teachers to undertake more than one or two of these transformations at any one time. In that case, it would not be appropriate to make use of all five scales when monitoring students' learning environment perceptions. There is no point in monitoring the absence of attributes of state B, especially if anomalous and misleading results are likely to be generated.

A similar problem is likely to occur if CLES scales are used too early in the monitoring of transformations to classroom learning environments (e.g., in the manner of a pretest). In the absence of desired attributes of state B, students' responses to CLES items might be inconsistent. For example, when considering the immediate relevance of the Egg Project to the world outside of school (which, by most accounts, seemed to lack this type of relevance) some students (with highly favourable attitudes) over-reported perceptions of relevance as a result of transcending their immediate experiential contexts and referring to imagined future careers. We therefore caution researchers to take care when adopting research designs that involve the use of the CLES to obtain measures of change in students' perceptions.

Finally, the trial of the CLES scales made us aware of a major problem associated with the use of negatively-worded items. We believe that some negatively-worded items yielded inconsistent responses from students partly because of the conceptual complexity that occurs when students consider the item in relation to negatively-worded categories (i.e., seldom, almost never) of the frequency response scale. Of course, this problem is exacerbated by the use of conceptually asymmetric items which, when reverse-scored, are assumed to contribute to a particular scale.

In this study, we encountered a classroom in which the learning environment was in a state of flux. Environments such as this pose challenges for learning environment researchers, and give rise to several important questions. First, can learning environment questionnaires stand alone as indicators of learning environments under transformation? Second, to what extent do the warrants of psychometric research (e.g., validity, homogeneity) provide adequate criteria for understanding the nature of a transforming learning environment? Third, what types of research design are best for teacher-researchers who wish to use learning environment questionnaires to transform their classroom learning environments?

References

Apple, M. (1979). Ideology and curriculum. London: Routledge and Kegan Paul.

Bauersfeld, H. (1988). Interaction, construction, and knowledge: Alternative perspectives for mathematics education. In D. A. Grouws & T. J. Cooney (Eds.), Perspectives on research on effective mathematics teaching (Vol. 1) (pp. 27-46). Reston, VA: The National Council of Teachers of Mathematics.

Bauersfeld, H. (1992, February). The structuring of the structures. Paper presented at the International Symposium on Alternative Epistemologies in Education, University of Georgia.

Berger, P. L. & Luckmann, T. (1966). The social construction of reality: A treatise in the sociology of knowledge. London: Penguin Books.

Burden, R., & Fraser, B.J. (in press). Use of classroom environment assessments in school psychology: A British perspective. Psychology in the Schools.

Chavez, R.C. (1984). The use of high inference measures to study classroom climates: A review. Review of Educational Research, 54, 237-261.

Cobb, P. (1989). Experiential, cognitive, and anthropological perspectives in mathematics education. For the Learning of Mathematics, 9(2), 32-42.

Davis, P. J. & Hersch, R. H. (1981). The mathematical experience. Boston: Birkhauser.

Denzin, N. K. (1988). Triangulation. In J.P. Keeves (Ed.), Educational research, methodology, and measurement: An international handbook (pp. 511-513). Sydney: Pergamon Press.

Dorman, J., Fraser, B.J., & McRobbie, C.J. (1994, April). Rhetoric and reality: A study of classrooms in Catholic and government secondary schools. Paper presented at the annual meeting of the AERA , New Orleans, LA.

Driver, R. (1988). Theory into practice II: A constructivist approach to curriculum development. In P. Fensham (Ed.), Development and dilemmas in science education. London: The Falmer Press.

Driver, R. (1990, April). Constructivist approaches to science teaching. Paper presented at University of Georgia, Mathematics Education Department as a contribution to the Seminar Series 'Constructivism in Education'.

Duschl, R.A & Gitomar, D. H. (1991). Epistemological perspectives on conceptual change: Implications for educational practice. Journal of Research in Science Teaching, 28, 839-858.

Eisenhart, M. A. (1988). The ethnographic research tradition and mathematics education research. Journal for Research in Mathematics Education, 19, 99-114.

Ernest, P. (1991). The philosophy of mathematics education. Hampshire, United Kingdom: The Falmer Press.

Ernest, P. (1992). The nature of mathematics: A social constructivist account. Science & Education, 1, 89-100.

Feyerabend, P. (1975). Against method. London: Verso.

Fraser, B.J. (1981). Learning environment in curriculum evaluation: A review (Evaluation in Education Series). Oxford, England: Pergamon Press.

Fraser, B.J. (1981). Test of science-related attitudes (TOSRA). Melbourne: Australian Council for Educational Research.

Fraser, B.J. (1982). Differences between student and teacher perceptions of actual and preferred classroom learning environment. Educational Evaluation and Policy Analysis, 4, 511-519.

Fraser, B.J. (1986). Classroom environment. London: Croom Helm.

Fraser, B.J. (1989). Twenty years on classroom environment work: Progress and prospect. Journal of Curriculum Studies, 21, 307-327.

Fraser, B.J. (1993). Incorporating classroom and school environment ideas into teacher education programs. In T.A. Simpson (Ed.), Teacher educators' annual handbook 1993 (pp. 135-152). Brisbane, Australia: Queensland University of Technology.

Fraser, B.J. (1994). Research on classroom and school climate. In D. Gabel (Ed.), Handbook of Research on Science Teaching and Learning (pp. 493-541). New York: Macmillan.

Fraser, B.J., & Fisher, D.L. (1982). Predicting students' outcomes from their perceptions of classroom psychosocial environment. American Educational Research Journal, 19, 498-518.

Fraser, B.J., & Fisher, D.L. (1983). Student achievement as a function of person-environment fit: A regression surface analysis. British Journal of Educational Psychology, 53, 89-99.

Fraser, B.J., & Fisher, D.L. (1986). Using short forms of classroom climate instruments to assess and improve classroom psychosocial environment. Journal of Research in Science Teaching, 23, 387-413.

Fraser, B.J., & Walberg, H.J. (Eds.) (1991). Educational Environments: Evaluation, antecedents and consequences. Oxford, England: Pergamon Press.

Fraser, B.J., Walberg, H.J., Welch, W.W., & Hattie, J.A. (1987). Syntheses of educational productivity research. International Journal of Educational Research, 11(2), 145-252 (whole issue).

Fraser, B.J., & Walberg, H.J. (Eds.) (1991). Educational environments: Evaluation, antecedents, and consequences. Oxford, England: Pergamon Press.

Fraser, B.J., Williamson, J.C., & Tobin, K. (1987). Use of classroom and school climate scales in evaluating alternative high schools. Teaching and Teacher Education, 3, 219-231.

Giroux, H.A. (1983). Critical theory and educational practice. Deakin University Press, Geelong, Victoria.

Grundy, S. (1987). Curriculum: Product or praxis? London: The Falmer Press.

Habermas, J. (1972). Knowledge and human interests (2nd ed.) (J. J. Shapiro, Trans.). London: Heinemann.

Habermas, J. (1984). A theory of communicative action: Vol 1. Reason and the rationalisation of society (T. McCarthy, Trans.). Boston: Beacon Press.

Haertel, G.D., Walberg, H.J., & Haertel, E.H. (1981). Socio-psychological environments and learning: A quantitative synthesis. British Educational Research Journal, 7, 27-36.

Heroman, D., Loup, K., Chauvin, S., & Evans, L. (1991, April). Student perceptions of the learning environment, on-the-job assessments of teaching and learning. Paper presented at annual meeting of American Educational Research Association, Chicago, IL.

Hersch, R. (1986). Some proposals for reviving the philosophy of mathematics. In T. Tymoczko (Ed.), New directions in the philosophy of mathematics (pp. 9-28). Boston: Birkhauser.

Kemmis, S. & Fitzclarence, L. (1986). Curriculum theorising: Beyond reproduction theory. Geelong, Victoria: Deakin University Press.

Kitcher, P. (1984). The nature of mathematical knowledge. Oxford, UK: Oxford University Press.

Kline, M. (1953). Mathematics in western culture. Oxford, UK: Oxford University Press.

Kline, M. (1980). Mathematics: The loss of certainty. Oxford, UK: Oxford University Press.

Kuhn, T.S. (1962). The structure of scientific revolutions (2nd ed.). Chicago: University of Chicago Press.

Kyle, D.W. & McCutcheon, G. (1984). Collaborative research: Development and issues. Journal of Curriculum Studies 16(2), 173-179.

MacAuley, D.J. (1990). Classroom environment: A literature review. Educational Psychology, 10, 239-253.

Mathison, S. (1988). Why triangulate? Educational Researcher, 17, 13-17.

McRobbie, C.J. & Fraser, B.J. (1993). Association between student outcomes and psychosocial science environments. Journal of Educational Research, 87, 78-85.

Midgley, C., Eccles, J.S., & Feldlaufer, H. (1991). Classroom environment and the transition to junior high school. In B.J. Fraser and H.J. Walberg (Eds.), Educational Environments: Evaluation, Antecedents and Consequences. Oxford, England: Pergamon Press.

Moos, R.H. (1979). Evaluating Educational Environments: Procedures, Measures, Findings and Policy Implications. San Francisco: Jossey-Bass.

Moos, R.H. (1991). Connections between school, work, and family settings. In B.J. Fraser and H.J. Walberg (Eds.), Educational Environments: Evaluation, Antecedents and Consequences. Oxford, England: Pergamon Press.

Polanyi, M. (1967). Science and reality. British Journal for the Philosophy of Science, 18, 177-196.

Raviv, Amiram, Raviv, Alona, & Reisel, E. (1990). Teacher and students: Two different perspectives?! Measuring social climate in the classroom. American Educational Research Journal, 27, 141-157.

Roth, W.M. & Roychoudhury, A. (1993). The nature of scientific knowledge, knowing and learning: The perspectives of four physics students. International Journal of Science Education, 15(1), 27-44.

Roth, W.M. & Roychoudhury, A. (1994). Physics students epistemologies and views about knowing and learning. Journal of Research in Science Teaching, 31, 5-30.

Roth, W.M. & Bowen, G.M. (in press). Knowing and interacting: A study of culture, practices, and resources in a grade 8 open-inquiry science classroom guided by a cognitive apprenticeship metaphor. Cognition and Instruction.

Schon, D. A. (1983). The reflective practitioner: How professionals think in action. USA: Basic Books.

Solomon, J. (1987). Social influences on the construction of pupils' understanding of science. Studies in Science Education, 14, 63-82.

Solomon, J. (1991). Images of physics: How students are influenced by social aspects of science. In R. Duit, F. Goldberg and H. Niedderer (Eds.), Research in physics learning: Theoretical issues and empirical studies (pp. 141-154). Proceedings of an International Workshop, University of Bremen (March, 1991): IPN, University of Kiel.

Taylor, P.C. (1992). An interpretive study of the role of teacher beliefs in the implementation of constructivist theory in a secondary mathematics classroom. Unpublished doctoral thesis, Curtin University, Perth, Australia.

Taylor, P.C. (1993). The influence of researcher beliefs on constructivist teaching practice. In K. Tobin (Ed.), The practice of constructivism in science and mathematics education. Washington, DC: American Association for the Advancement of Science.

Taylor, P.C. (1994). Mythmaking and mythbreaking in the mathematics classroom. SMEC, Curtin University of Technology.

Taylor, P.C. & Fraser, B.J. (1991, April). Development of an instrument for assessing constructivist learning environments. Paper presented at the annual meeting of the American Educational Research Association, New Orleans, L.A..

Taylor, P. & Campbell-Williams, M. (1993). Discourse toward balanced rationality in the high school mathematics classroom: Ideas from Habermas's critical theory. In J.A. Malone & P.C.S. Taylor (Eds.), Constructivist interpretations of teaching and learning mathematics (Proceeding of Topic Group 10 at the Seventh International Congress on Mathematical Education) (pp. 135-148). Perth, Western Australia: Curtin University of Technology.

Tobin, K. (1990). Social constructivist perspectives on the reform of science education. Australian Science Teachers Journal, 36(4), 29-35.

Tobin, K. (Ed.) (1993). The practice of constructivism in science education. Washington, DC: Association for the Advancement of Science (AAAS) Press.

Toulmin, S. (1953). The philosophy of science: An introduction. London: Hutchinson.

Treagust, D., Duit, R., & Fraser, B. (Eds.), (in press). Teaching and learning in science and mathematics. New York: Teachers College Press.

Trickett, E.J., Trickett, P.K., Castro, J.J., & Schaffner, P. (1982). The independent school experience: Aspects of normative environments of single sex and coed schools. Journal of Educational Psychology, 74, 374-381.

von Glasersfeld, E. (1990). An exposition of constructivism: Why some like it radical. In R.B. Davis, C.A. Maher, & N. Noddings (Eds.), Constructivist views on the teaching and learning of mathematics. Journal of Research in Mathematics Education Monographs, 4, 19-29. Reston, VA: National Council of Teachers of Mathematics.

von Glasersfeld, E. (1990). Questions and answers about radical constructivism. In K. Tobin (Ed.), The practice of constructivism in science education (pp. 23-38). Washington, DC: Association for the Advancement of Science (AAAS) Press

Watt, D.H. & Watt, H. (1982). Design criteria for collaborative classroom research. In T.M. Amabile & M.L. Stubbs (Eds.), Psychological research in the classroom (pp. 134-143). Brandeis University: Pergamon Press.

Watters, J.J. & Ginns, I.S. (1994). Self-efficacy and science anxiety among preservice primary teachers: Origins and remedies. Queensland University of Technology.

Wubbels, Th., Brekelmans, M., & Hooymayers, H. (1991). Interpersonal teacher behavior in the classroom. In B.J. Fraser and H.J. Walberg (Eds.), Educational environments: Evaluation, antecedents and consequences. Oxford, England: Pergamon Press.

APPENDIX

mathematics CLASSROOM LEARNING ENVIRONMENT SURVEY

STUDENT PERCEPTIONS

directions

1. This questionnaire asks you to describe this classroom which you are in right now. There are no right or wrong answers. This is not a test. Your opinion is what is wanted.

2. Do not write your name. Your answers are confidential and anonymous.

3. On the next few pages you will find 48 sentences. For each sentence, circle one number corresponding to your answer.

For example:

		Almost Always	Often	Some-times	Seldom	Almost Never
In this class . . .
	the teacher asks me questions.	5	4	3	2	1

• If you think this teacher almost always asks you questions, circle the 5.

• If you think this teacher almost never asks you questions, circle the 1.

• Or you can choose the number 2, 3 or 4 if this seems like a more accurate answer.

4. If you want to change your answer, cross it out and circle a new number, e.g.:

3

2

1

5. Please provide details in the box below:

a. School:	b. Teacher's Name:
c. Subject:	d. Grade/Level:
e. Your Sex (please circle): Male or Female

6. Now turn the page and please give an answer for every question.

		Almost Always	Often	Some-times	Seldom	Almost Never
In this class . . .
1	I learn about the world outside of school.	5	4	3	2	1
2	I learn that mathematics cannot provide perfect answers.	5	4	3	2	1
3	It's OK to ask the teacher "why do we have to learn this?"	5	4	3	2	1
In this class . . .
4	I help the teacher to plan what I'm going to learn.	5	4	3	2	1
5	I get the chance to talk to other students.	5	4	3	2	1
6	I look forward to the learning activities.	5	4	3	2	1
In this class . . .
7	New learning starts with problems about the world outside of school.	5	4	3	2	1
8	I learn how mathematics has changed over time.	5	4	3	2	1
9	I feel free to question the way I'm being taught.	5	4	3	2	1
		Almost Always	Often	Some-times	Seldom	Almost Never
In this class . . .
10	I help the teacher decide how well my learning is going.	5	4	3	2	1
11	I talk with other students about how to solve problems.	5	4	3	2	1
12	The activities are among the most interesting at this school.	5	4	3	2	1
In this class . . .
13	I learn how mathematics can be part of my out-of-school life.	5	4	3	2	1
14	I learn how the rules of mathematics were invented.	5	4	3	2	1
15	It's OK to complain about activities that are confusing.	5	4	3	2	1
In this class . . .
16	I have a say in deciding the rules for classroom discussion.	5	4	3	2	1
17	I try to make sense of other students' ideas.	5	4	3	2	1
18	The activities make me interested in mathematics.	5	4	3	2	1
		Almost Always	Often	Some-times	Seldom	Almost Never

		Almost Always	Often	Some-times	Seldom	Almost Never
In this class . . .
19	I get a better understanding of the world outside of school.	5	4	3	2	1
20	I learn about the different mathematics used by people in other cultures.	5	4	3	2	1
21	It's OK to complain about anything that stops me from learning.	5	4	3	2	1
In this class . . .
22	I have a say in deciding how much time I spend on an activity.	5	4	3	2	1
23	I ask other students to explain their ideas.	5	4	3	2	1
24	I enjoy the learning activities.	5	4	3	2	1
In this class . . .
25	I learn interesting things about the world outside of school.	5	4	3	2	1
26	I learn that mathematics is just one of many ways of understanding the world.	5	4	3	2	1
27	I'm free to express my opinion.	5	4	3	2	1
		Almost Always	Often	Some-times	Seldom	Almost Never
In this class . . .
28	Other students ask me to explain my ideas.	5	4	3	2	1
29	I feel confused.	5	4	3	2	1
30	What I learn has nothing to do with my out-of-school life.	5	4	3	2	1
In this class . . .
31	I learn that today's mathematics is different from the mathematics of long ago.	5	4	3	2	1
32	It's OK to speak up for your rights.	5	4	3	2	1
33	I have a say in deciding what will be on the test.	5	4	3	2	1
In this class . . .
34	Other students explain their ideas to me.	5	4	3	2	1
35	The learning activities are a waste of time.	5	4	3	2	1
36	I have a say in deciding what activities I do.	5	4	3	2	1
		Almost Always	Often	Some-times	Seldom	Almost Never

		Almost Always	Often	Some-times	Seldom	Almost Never
In this class . . .
37	What I learn has nothing to do with the world outside of school.	5	4	3	2	1
38	I learn that mathematics is about inventing rules.	5	4	3	2	1
39	I feel unable to complain about anything.	5	4	3	2	1
In this class . . .
40	I have a say in deciding how my learning is assessed.	5	4	3	2	1
41	Other students pay attention to my ideas.	5	4	3	2	1
42	I feel tense.	5	4	3	2	1
		Almost Always	Often	Some-times	Seldom	Almost Never